More about TVM

Introduction TVM on HP 12c

Many financial problems are based on the concept of charging a fee (interest) for the use of someone else’s money for a fixed period of time. The phrase time value of money describes the calculations based on such problems.

There are two main types of financial problems that HP 12c can help to solve:

• Compound interest
• Simple interest

With simple interest, only the principal (the original amount of money) earns interest for the entire life of the transaction. The principal, plus interest earned is repaid in one lump sum.

When simple interest is added to the principal at specified compounding intervals, and thereafter, also earns interest, the interest is compounded. Savings accounts, mortgages and leases are compound-interest calculations.

TVM Elements

There are five standard variables used to describe most compound interest (TVM) problems:

n

Number of payments

i

Periodic interest rate

PV

Present value

PMT

Payment amount each period (periodic payment amount)

FV

Future value

The TVM capability in the HP 12C calculator does many compound-interest problems. Specifically, the TVM functionality can be used for a series of cash flows (money paid, or money received) when:

• The dollar amount is the same each payment
• The payments occur at regular intervals
• The payment period coincides with the compounding periods

Given any four of the above key elements, it is possible to solve for the fifth variable.

Cash Flow Diagrams and Signs of Numbers

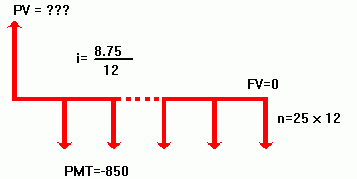
It is often helpful to illustrate or visualize TVM calculations with cash-flow diagrams. Cash-flow diagrams are time lines divided into equal segments called compounding (payment) periods. Arrows show the occurrence of cash flows (payment in or out). Money received is a positive number shown as an arrow pointing up, and money paid out is a negative number shown as an arrow pointing down (Figure 1).

It is essential to use the correct sign (positive or negative) for TVM numbers. The calculations will only make sense if payments out are consistently shown as negative, and payments in (receipts) as positive. A calculation must be performed from the point of view of either the lender (investor) or the borrower, but not both. This is called the TVM sign convention.

HP 12c TVM Example

Example: A home mortgage

The maximum monthly mortgage repayment you can make is $850. You can make a $14,000 down payment. The current interest rate is 8.75%. For a mortgage of 25 years, what is the maximum purchase price that you can afford?

Figure 1: Cash Flow Diagram

Following are the hp12c keystrokes used to solve the problem in this example problem:

Keystrokes

Display

Notes

[f][CLEAR FIN]

(the display is not changed)

Clear hp12c financial registers

[g][END]

(the display is not changed)

Set hp12c END mode

25 [g][12x]

300.00

Number of payments use by the hp 12c

8.75 [g][12x]

0.73

Monthly interest rate on the hp 12c

850 [CHS][PMT]

-850.00

Monthly payment on the hp12c

0 [FV]

0.00

Future value = 0

(ie mortgage paid out)

[PV]

103,388.26

Calculate amount to borrow

14000 [+]

117,388.26

Add down payment to get maximum purchase price.

Here is how to solve the same problem using the HP 10bii.

HP 12c TVM Tips

Following are some HP 12c tips to use when solving TVM problems, to help arrive at the correct answer:

• Clear the HP 12c TVM variables before beginning a new calculation. This removes unwanted values from the calculator memory.
• Set HP 12c the appropriate payment mode. (Mortgages and loans are typically END mode calculations, and leases are typically BEGIN mode calculations.
• Be sure the correct interest rate is entered into the HP 12c.
• The compounding period on the hp 12c must be the same as the payment period. (If not, interest rate conversion functions will need to be used to calculate the correct rate).
• Remember the sign convention on the hp12c:

money received = positive number, money paid out = negative number