HP 12c (platinum) - Calculating a Compound Annual Growth Rate
Introduction
Compound Annual Growth Rate (CAGR) is a measure of the rate of return on an investment. The CAGR is often calculated to determine the change in the value of a stock or property. If there is a negative or zero value for the first or last year, the growth is not meaningful.
The year over year growth rate of an investment over a specified period of time. Calculated by taking the nth root of the total percentage growth rate where n is the number of years in the period being considered.
This can be written as:
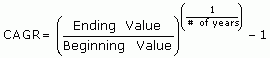
The mathematical formula that provides a ‘smoothed’ rate of return. It is really a projected number that tells you what an investment yields on an annually compounded basis; it indicates to investors what they really have at the end of the investment period.
Beginning and ending values are known
To calculate the compound annual growth rate when the beginning and ending values are known, follow these steps:
- Press 0, then PMT.
- Key in the beginning value, press CHS, and then PV.
- Key in the ending value, and press FV.
- Key in the number of periods between the beginning and ending values, and then press n.
- Press i to calculate the compound annual growth rate.
Multiple rates of return
To calculate the compound annual growth rate when multiple rates of return are involved, use the following procedure:
- Press 0, then PMT.
- Key in the beginning value, press CHS, PV, and then CHS. (If the beginning value is unknown, use $1.)
- Add or subtract each year’s return using the % (percent) key. Repeat this step for each rate of return.
- When each rate of return has been included, press FV to store the sum.
- Key in the number of years, and then press n.
- Press i to calculate the compound annual growth rate.
Example of a compound growth of a property
Ten years ago you purchased a home for $43,000. You have just sold it for $89,800. What is the periodic rate of appreciation?
Keys
Display
Description
Press 0, then PMT
0.00
Stores 0 in PMT
Type 43000, press CHS, then PV
-43,000.00
Stores beginning value
Type 89800, then press FV
89,800.00
Stores ending value
Type 10, then press n
10.00
Stores number of years
Press i
7.64
Calculates annual appreciation rate
Example of the growth rate on a fund
What is the annual yield or compound growth rate of a fund that has had the following annual returns?
Year 1
5%
Year 2
15%
Year 3
-3%
Year 4
8%
Keys
Display
Description
Press 0, then PMT
0.00
Stores 0 in PMT
Press 1, CHS, then PV
-1.00
Stores $1 as initial investment
Press CHS
1.00
Press 5, %, then +
1.05
Adds return for year 1
Type 15, then press %, then +
1.21
Adds return for year 2
Press 3, CHS, %, then +
1.17
Subtracts return for year 3
Press 8, %, then +
1.26
Adds return for year 4
Press FV
1.26
Stores amount at end of term
Press 4, then n
4.00
Stores number of years
Press i
6.05
Calculates annual yield
Here’s an example. I’ll use big numbers to exaggerate the kinds of errors you get if you don’t use CAGR:
Say you invest $1,000, and in your first year it goes up 100%. In one year, your initial investment has doubled to $2,000. Then in year two, things go poorly, and you lose 50%, and your $2,000 has shrunk back down to $1,000.
Now, if you simply averaged your percentage returns, you’d get:
100% (year one) plus a negative 50% (year two) equals 50%, divided by 2 = 25%.
Obviously, this isn’t right. You started with $1,000 and ended with $1,000. Your return wasn’t 25% per year, it was zero.
Enter CAGR.
To get the CAGR, you start with the total return and then figure out what one number, if used as the return each year, would have gotten you to that point. The compound annual growth rate doesn’t represent reality; instead it describes the rate at which your account grew as though it had grown at a steady rate. Here’s how it works.
Once again, you start with $1,000, but this time, let’s assume your account grows to $3,000. Your return for the first year was 200%, right? In year two, you lose 50%, and your account drops to $1,500. Since you made $500, half of $1,000, obviously you have a total return of 50% over the two years. So the question is: What consistent yearly return would have gotten you from $1,000 to $1,500 over a two-year period? That will be the CAGR.
We already know that you can’t just use the arithmetic mean of the yearly returns as your average return per year. In this case the mean works out to 75% per year, which is nuts considering that the total return was just 50%. But you also can’t simply divide the total return by two, either. That would be 25% per year, which is close, but no cigar. A 25% return the first year would take your account to $1,250, but a 25% return on that $1,250 in the second year would be $312.5 ($1250 x 0.25), giving you a total of $1562.50. Too much. Simply dividing the total return by the number of years doesn’t take compounding into effect. You have to ‘annualize’ the total return.
Let’s take a closer look at that math. We said a 25% return in the first year would take your account to $1,250. You can calculate that two ways: $1,000 X 0.25 = $250 + $1,000 = $1,250 or $1,000 x 1.25 = $1,250. Forgive the fourth-grade math review, but it’s important when calculating CAGR to use the second method. The 1 represents each year’s starting amount and you need to keep that initial amount in every calculation. It’s like when you calculate a tip. You can calculate the tip by multiplying the bill by 20% (0.20) but if you want to know the total cost of the meal including the tip, you multiply by 1.20.
To find the CAGR, you must start with the total return. One way to find the total return is to multiply all the yearly returns using the format 1 plus the annual return written as a decimal instead of a percentage (i.e., 200% written as a decimal is 2.00, 50% written as a decimal is 0.50). So in this example the first year multiplier is 1 plus 2.00 (which is what, class?), and the second year multiplier is 1 plus -0.50 which equals 0.50.
$1,000 x 3.00 x 0.50 = $1,500. This is the total return in dollar terms.
The total percentage return is 3.00 x 0.50 = 1.50 (normally written as a 50% return – the one is ignored).
That checks. You started with $1,000, and ended with $1,500, and your account went up 50% over the two-year time span. Another way to calculate the total return is: (Ending Value minus Starting Value) divided by the Starting Value. In this case:
$1,500 - $1,000 = $500
$500/$1,000 = 0.5 or 50%
If you use this method, you have to add 1 to the decimal answer. Gotta keep that starting amount in there. You will need it later on.
Now you are ready to calculate the CAGR. You start with the total return – in this example, 1.50. Then you take the X root, where X is the number of years. We are using a two-year example, so we would take the square root. The square root of 1.50 is 1.225 which translates to an average return of 22.5% once we get rid of the starting amount (represented by 1) and change it to a decimal.
Let’s see if this works. Start with $1,000 and increase it by 22.5% per year.
$1,000 x 1.225 x 1.225 = $1,500.625 (the 62.5 cents is due to rounding errors. The actual return was 1.22474487139158904909864203735295, but that is a bit over-precise).
Here’s another example. Start with $1,000. In year one you get a 20% return ($1,200 at year end). In year two you go up another 10% ($1,320 at end of year two), down 15% in year three ($1,122), and up 30% in year four ($1,458.60 ending amount).
Multiply the returns for each year to get the total return.
1.20 * 1.10 * 0.85 * 1.30 = 1.4586 (or 45.86%)
Now, all we need is the CAGR. For two years we took the square root. For three years, you would take the cube root. For four years, that’s the… quad root or something? I just use my trusty spreadsheet to do these calculations. Spreadsheets and some calculators take roots by using the inverse of the root as an exponent, so a square root is 1/2, a cube root is 1/3, etc. In this example, that’s:
1.4586^(1/4), or 1.4586^0.25, which equals 1.099.
1.099 - 1= 0.099, or 9.9%.
Your eyes are glazing over, aren’t they? We’re almost done. Unless you want to calculate your portfolio performance, you don’t have to remember all the math. Just remember the concept this way. Whether you put $1,000 in a bank account that paid 9.9%, compounded annually, or into a stock strategy like the one above that has a CAGR of 9.9%, after four years your $1,000 would grow to $1,458.60. That’s exactly what ‘Compound Annual Growth Rate’ means.